Comparison of Calibration of Classifiers¶
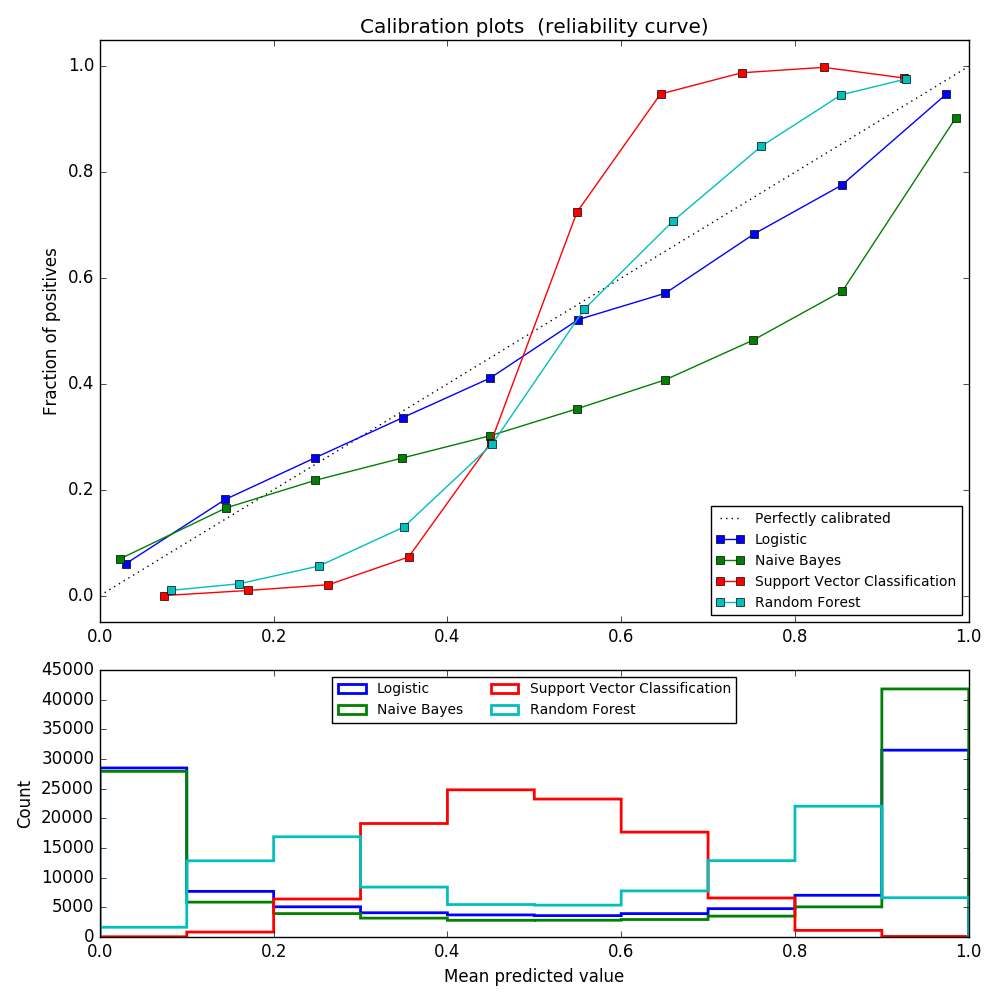
Well calibrated classifiers are probabilistic classifiers for which the output of the predict_proba method can be directly interpreted as a confidence level. For instance a well calibrated (binary) classifier should classify the samples such that among the samples to which it gave a predict_proba value close to 0.8, approx. 80% actually belong to the positive class.
LogisticRegression returns well calibrated predictions as it directly optimizes log-loss. In contrast, the other methods return biased probilities, with different biases per method:
- GaussianNaiveBayes tends to push probabilties to 0 or 1 (note the counts in the histograms). This is mainly because it makes the assumption that features are conditionally independent given the class, which is not the case in this dataset which contains 2 redundant features.
- RandomForestClassifier shows the opposite behavior: the histograms show peaks at approx. 0.2 and 0.9 probability, while probabilities close to 0 or 1 are very rare. An explanation for this is given by Niculescu-Mizil and Caruana [1]: “Methods such as bagging and random forests that average predictions from a base set of models can have difficulty making predictions near 0 and 1 because variance in the underlying base models will bias predictions that should be near zero or one away from these values. Because predictions are restricted to the interval [0,1], errors caused by variance tend to be one- sided near zero and one. For example, if a model should predict p = 0 for a case, the only way bagging can achieve this is if all bagged trees predict zero. If we add noise to the trees that bagging is averaging over, this noise will cause some trees to predict values larger than 0 for this case, thus moving the average prediction of the bagged ensemble away from 0. We observe this effect most strongly with random forests because the base-level trees trained with random forests have relatively high variance due to feature subseting.” As a result, the calibration curve shows a characteristic sigmoid shape, indicating that the classifier could trust its “intuition” more and return probabilties closer to 0 or 1 typically.
- Support Vector Classification (SVC) shows an even more sigmoid curve as the RandomForestClassifier, which is typical for maximum-margin methods (compare Niculescu-Mizil and Caruana [1]), which focus on hard samples that are close to the decision boundary (the support vectors).
References:
| [1] | Predicting Good Probabilities with Supervised Learning, A. Niculescu-Mizil & R. Caruana, ICML 2005 |
Python source code: plot_compare_calibration.py
print(__doc__)
# Author: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD Style.
import numpy as np
np.random.seed(0)
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
from sklearn.calibration import calibration_curve
X, y = datasets.make_classification(n_samples=100000, n_features=20,
n_informative=2, n_redundant=2)
train_samples = 100 # Samples used for training the models
X_train = X[:train_samples]
X_test = X[train_samples:]
y_train = y[:train_samples]
y_test = y[train_samples:]
# Create classifiers
lr = LogisticRegression()
gnb = GaussianNB()
svc = LinearSVC(C=1.0)
rfc = RandomForestClassifier(n_estimators=100)
###############################################################################
# Plot calibration plots
plt.figure(figsize=(10, 10))
ax1 = plt.subplot2grid((3, 1), (0, 0), rowspan=2)
ax2 = plt.subplot2grid((3, 1), (2, 0))
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
for clf, name in [(lr, 'Logistic'),
(gnb, 'Naive Bayes'),
(svc, 'Support Vector Classification'),
(rfc, 'Random Forest')]:
clf.fit(X_train, y_train)
if hasattr(clf, "predict_proba"):
prob_pos = clf.predict_proba(X_test)[:, 1]
else: # use decision function
prob_pos = clf.decision_function(X_test)
prob_pos = \
(prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
fraction_of_positives, mean_predicted_value = \
calibration_curve(y_test, prob_pos, n_bins=10)
ax1.plot(mean_predicted_value, fraction_of_positives, "s-",
label="%s" % (name, ))
ax2.hist(prob_pos, range=(0, 1), bins=10, label=name,
histtype="step", lw=2)
ax1.set_ylabel("Fraction of positives")
ax1.set_ylim([-0.05, 1.05])
ax1.legend(loc="lower right")
ax1.set_title('Calibration plots (reliability curve)')
ax2.set_xlabel("Mean predicted value")
ax2.set_ylabel("Count")
ax2.legend(loc="upper center", ncol=2)
plt.tight_layout()
plt.show()
Total running time of the example: 3.28 seconds ( 0 minutes 3.28 seconds)

