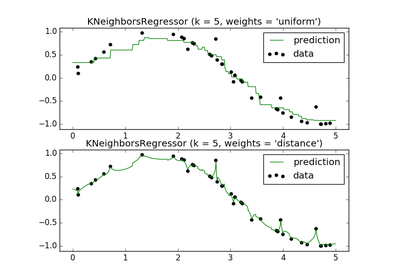
sklearn.neighbors.KNeighborsRegressor¶
-
class
sklearn.neighbors.KNeighborsRegressor(n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=1, **kwargs)[源代码]¶ Regression based on k-nearest neighbors.
The target is predicted by local interpolation of the targets associated of the nearest neighbors in the training set.
Read more in the User Guide.
Parameters: n_neighbors : int, optional (default = 5)
Number of neighbors to use by default for
k_neighborsqueries.weights : str or callable
weight function used in prediction. Possible values:
- ‘uniform’ : uniform weights. All points in each neighborhood are weighted equally.
- ‘distance’ : weight points by the inverse of their distance. in this case, closer neighbors of a query point will have a greater influence than neighbors which are further away.
- [callable] : a user-defined function which accepts an array of distances, and returns an array of the same shape containing the weights.
Uniform weights are used by default.
algorithm : {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, optional
Algorithm used to compute the nearest neighbors:
- ‘ball_tree’ will use
BallTree - ‘kd_tree’ will use
KDtree - ‘brute’ will use a brute-force search.
- ‘auto’ will attempt to decide the most appropriate algorithm
based on the values passed to
fitmethod.
Note: fitting on sparse input will override the setting of this parameter, using brute force.
leaf_size : int, optional (default = 30)
Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
metric : string or DistanceMetric object (default=’minkowski’)
the distance metric to use for the tree. The default metric is minkowski, and with p=2 is equivalent to the standard Euclidean metric. See the documentation of the DistanceMetric class for a list of available metrics.
p : integer, optional (default = 2)
Power parameter for the Minkowski metric. When p = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used.
metric_params : dict, optional (default = None)
Additional keyword arguments for the metric function.
n_jobs : int, optional (default = 1)
The number of parallel jobs to run for neighbors search. If
-1, then the number of jobs is set to the number of CPU cores. Doesn’t affectfitmethod.Notes
See Nearest Neighbors in the online documentation for a discussion of the choice of
algorithmandleaf_size.警告
Regarding the Nearest Neighbors algorithms, if it is found that two neighbors, neighbor k+1 and k, have identical distances but but different labels, the results will depend on the ordering of the training data.
http://en.wikipedia.org/wiki/K-nearest_neighbor_algorithm
Examples
>>> X = [[0], [1], [2], [3]] >>> y = [0, 0, 1, 1] >>> from sklearn.neighbors import KNeighborsRegressor >>> neigh = KNeighborsRegressor(n_neighbors=2) >>> neigh.fit(X, y) KNeighborsRegressor(...) >>> print(neigh.predict([[1.5]])) [ 0.5]
Methods
fit(X, y)Fit the model using X as training data and y as target values get_params([deep])Get parameters for this estimator. kneighbors([X, n_neighbors, return_distance])Finds the K-neighbors of a point. kneighbors_graph([X, n_neighbors, mode])Computes the (weighted) graph of k-Neighbors for points in X predict(X)Predict the target for the provided data score(X, y[, sample_weight])Returns the coefficient of determination R^2 of the prediction. set_params(**params)Set the parameters of this estimator. -
__init__(n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=1, **kwargs)[源代码]¶
-
fit(X, y)[源代码]¶ Fit the model using X as training data and y as target values
Parameters: X : {array-like, sparse matrix, BallTree, KDTree}
Training data. If array or matrix, shape [n_samples, n_features], or [n_samples, n_samples] if metric=’precomputed’.
y : {array-like, sparse matrix}
- Target values, array of float values, shape = [n_samples]
or [n_samples, n_outputs]
-
get_params(deep=True)[源代码]¶ Get parameters for this estimator.
Parameters: deep: boolean, optional :
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
-
kneighbors(X=None, n_neighbors=None, return_distance=True)[源代码]¶ Finds the K-neighbors of a point.
Returns indices of and distances to the neighbors of each point.
Parameters: X : array-like, shape (n_query, n_features), or (n_query, n_indexed) if metric == ‘precomputed’
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
n_neighbors : int
Number of neighbors to get (default is the value passed to the constructor).
return_distance : boolean, optional. Defaults to True.
If False, distances will not be returned
Returns: dist : array
Array representing the lengths to points, only present if return_distance=True
ind : array
Indices of the nearest points in the population matrix.
Examples
In the following example, we construct a NeighborsClassifier class from an array representing our data set and ask who’s the closest point to [1,1,1]
>>> samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=1) >>> neigh.fit(samples) NearestNeighbors(algorithm='auto', leaf_size=30, ...) >>> print(neigh.kneighbors([[1., 1., 1.]])) (array([[ 0.5]]), array([[2]]...))
As you can see, it returns [[0.5]], and [[2]], which means that the element is at distance 0.5 and is the third element of samples (indexes start at 0). You can also query for multiple points:
>>> X = [[0., 1., 0.], [1., 0., 1.]] >>> neigh.kneighbors(X, return_distance=False) array([[1], [2]]...)
-
kneighbors_graph(X=None, n_neighbors=None, mode='connectivity')[源代码]¶ Computes the (weighted) graph of k-Neighbors for points in X
Parameters: X : array-like, shape (n_query, n_features), or (n_query, n_indexed) if metric == ‘precomputed’
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
n_neighbors : int
Number of neighbors for each sample. (default is value passed to the constructor).
mode : {‘connectivity’, ‘distance’}, optional
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, in ‘distance’ the edges are Euclidean distance between points.
Returns: A : sparse matrix in CSR format, shape = [n_samples, n_samples_fit]
n_samples_fit is the number of samples in the fitted data A[i, j] is assigned the weight of edge that connects i to j.
Examples
>>> X = [[0], [3], [1]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=2) >>> neigh.fit(X) NearestNeighbors(algorithm='auto', leaf_size=30, ...) >>> A = neigh.kneighbors_graph(X) >>> A.toarray() array([[ 1., 0., 1.], [ 0., 1., 1.], [ 1., 0., 1.]])
-
predict(X)[源代码]¶ Predict the target for the provided data
Parameters: X : array-like, shape (n_query, n_features), or (n_query, n_indexed) if metric == ‘precomputed’
Test samples.
Returns: y : array of int, shape = [n_samples] or [n_samples, n_outputs]
Target values
-
score(X, y, sample_weight=None)[源代码]¶ Returns the coefficient of determination R^2 of the prediction.
The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.
Parameters: X : array-like, shape = (n_samples, n_features)
Test samples.
y : array-like, shape = (n_samples) or (n_samples, n_outputs)
True values for X.
sample_weight : array-like, shape = [n_samples], optional
Sample weights.
Returns: score : float
R^2 of self.predict(X) wrt. y.