1. Introduction
  2. Related work
  3. Adversarial nets
  4. Theoretical Results
    1. Global Optimality of \(p_g = p_{data}\)
    2. Convergence of Algorithm 1
  5. Experiments
  6. Advantages and disadvantages
  7. Conclusions and future work

(NIPS 2014) Generative Adversarial Nets
Paper: https://papers.nips.cc/paper/5423-generative-adversarial-nets
Code: http://www.github.com/goodfeli/adversarial

We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that a sample came from the training data rather than G.

The training procedure for G is to maximize the probability of D making a mistake.

This framework corresponds to a minimax two-player game.

Introduction

Deep generative models have had less of an impact, due to the difficulty of approximating many intractable probabilistic computations that arise in maximum likelihood estimation and related strategies, and due to difficulty of leveraging the benefits of piecewise linear units in the generative context.

We propose a new generative model estimation procedure that sidesteps these difficulties.

The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency.

we can train both models using only the highly successful backpropagation and dropout algorithms [17] and sample from the generative model using only forward propagation. No approximate inference or Markov chains are necessary.

Adversarial nets

D and G play the following two-player minimax game with value function \(V (G, D)\):

\[\min_G \max_D V(D,G) = \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [\log (1 - D(G(z)))]\]

Optimizing D to completion in the inner loop of training is computationally prohibitive, and on finite datasets would result in overfitting. Instead, we alternate between k steps of optimizing D and one step of optimizing G.

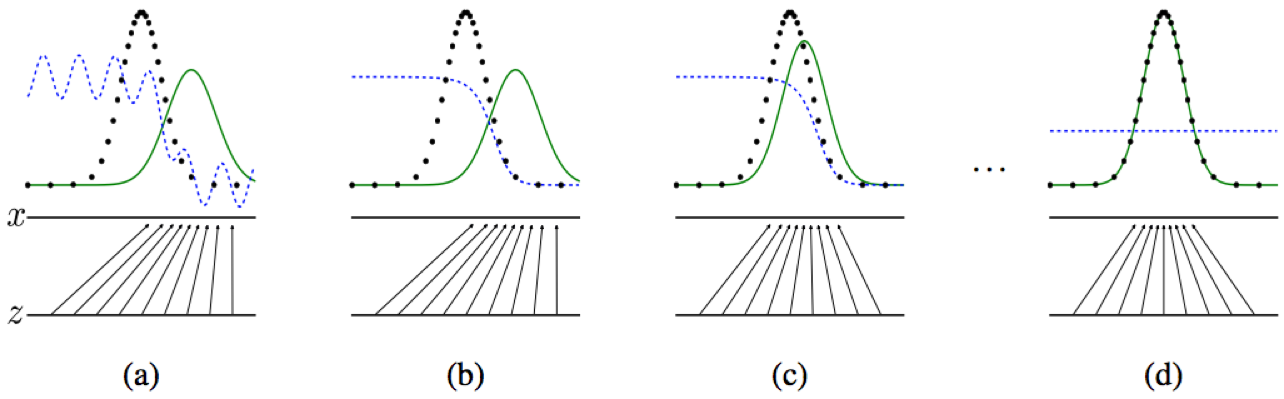
Figure 1: Generative adversarial nets are trained by simultaneously updating the discriminative distribution (D, blue, dashed line) so that it discriminates between samples from the data generating distribution (black, dotted line) \(p_x\) from those of the generative distribution \(p_g\) (G) (green, solid line).

The lower horizontal line is the domain from which \(z\) is sampled, in this case uniformly.

The horizontal line above is part of the domain of \(x\).

The upward arrows show how the mapping \(x = G(z)\) imposes the non-uniform distribution \(p_g\) on transformed samples.

G contracts in regions of high density and expands in regions of low density of \(p_g\).

  1. Poorly fit model

  2. After updating D

  3. After updating G

  4. Mixed strategy equilibrium

Theoretical Results

Global Optimality of \(p_g = p_{data}\)

Convergence of Algorithm 1

Experiments

We trained adversarial nets an a range of datasets including MNIST[23], the Toronto Face Database (TFD) [28], and CIFAR-10 [21].

Advantages and disadvantages

Conclusions and future work